The more concentrated the smaller the standard. Standard Deviation of a given set of observations is defined as the positive square root of the arithmetic mean of the squares of deviations of the observations from their arithmetic mean.

Ex Interpret The Mean And Standard Deviation Of Two Data Sets Youtube
Standard Deviation.
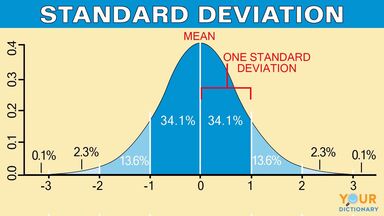
. It is an absolute measure of dispersion. Standard deviation 𝒙𝒙 𝒏 _____. The standard deviation or confidence interval can also be.
Standard this refers to the standard or typicaldistance that a value is from the mean. It is a measure of dispersion of observation within dataset relative to their meanIt is square root of the variance and denoted by Sigma σ. More precisely it is a measure of the average distance between the values of the data in the set and the mean.
To describe our data the mean alone doesnt provide enough information. It is a single number that tells us the variability or spread of a distribution group of scores. Describe the mean and standard deviation in words after calculating it.
The mean is a measure of central tendency of a distribution while the SD is a measure of dispersion of its scores. 𝑥𝑥2 𝑛1 Final Step. DataFramedescribe calls Seriesstd to get the standard deviation.
The formula to find the variance of a. Describe the mean spread standard deviation and shape of a distribution of means assuming the population mean and standard deviation are known. When the standard deviation is large the scores are more widely spread out.
Describe its programs and give one example of an output and an outcome it showcases to describe its impact and effectiveness. X sample mean. Basically a small standard deviation means that the values in a statistical data set are close to the mean or average of the data set and a large standard deviation means that the values in the data set are farther away from the mean.
The smaller the standard deviation the closer the scores are on average to the mean. The standard deviation of a data set describes the difference between the data in the set and their mean. Select the key concepts in the chapters that are most significant or meaningful to you.
Mean_____ n_____ Sum of Difference from the Mean 2 divided by degrees of freedom n 1 _____ This is called variance. This can be changed using the ddof argument. - is shorthand for plus or minus ie.
Subtract the mean x from each value. It might be zero if all the data values are equal. The scaling uses the mean and the standard deviation for each variable computed on the training set.
Describe mean standard Deviation. When the elements in a series are more isolated from the mean then the standard. Frequencies range percentile and standard deviation are used for descriptive statistics.
So the standard deviation of 17 is the square root of the average. Standard deviation is considered the most useful index of variability. A low standard deviation indicates that the data points tend to be very close to the mean.
-SD can never be negative. Also assume that each sample in the distribution of means has 45 people in it. Many statistical analyses use the mean as a standard measure of the center of the distribution of the data.
Once you understand standard deviation its much easier to understand variance. The standard deviation of 17 shows how much dispersion there is from the mean wage. Could be greater than or less than this value.
But the values could be - 1 or - 100 of that value. Test Score x Difference from the mean x x Difference from the mean x2 Sum of Difference from the mean x. Standard deviation denoted by the symbol σ describes the square root of the mean of the squares of all the values of a series derived from the arithmetic mean which is also called the root-mean-square deviation.
Precisely the standard deviation is the square root of the variance which is the average of the squared differences from the mean. With samples we use n 1 in the formula because using n would give us a biased estimate that consistently underestimates variability. You dont have to calculate specific numbers but tell me in words what to expect the mean SD and shape to look like.
Standard deviation square root of what you just calculated variance. The median and the mean both measure central tendency. The sample standard deviation would tend to be lower than the real standard deviation of the population.
The standard deviation abbreviated to SD is a measure of variation based on measuring how far each data value deviates from the mean. In order to determine standard deviation. The standard deviation of a data set describes how much do the data differ from their mean.
Mean to describe the sample with a single value that represents the center of the data. A high standard deviation indicates that the data points are spread out over a large range of values. How do you interpret mean and standard deviation.
Latexdisplaystyle sigma_textmean fracsigmasqrttextNlatex. Standard Deviation is calculated by. Take the mean from the score.
This is shown in the SD numbers where empowerment showed a difference of 011 902-891011. I would say that this suggests that wages are very spread out. N number of values in the sample.
Show activity on this post. So the standard deviation returned by describe is in fact the corrected sample standard deviation. And as the documentation tells us Return unbiased standard deviation over requested axis.
It tells us what value we should observe on average. Mean Standard Deviation Z Scores Correlation Finally if someone told you that the average of a data set was 40 and that standard deviation was 10 what else could you derive from that information. But unusual values called outliers affect the median less than they affect the mean.
Often we want some information about the precision of the mean we obtained. Describe the following terms in your own words. 0 is the smallest value of standard deviation since it cannot be negative.
The standard deviation measures how concentrated the data are around the mean. Standard deviation is the measure of spreading of numerical data about an average. Normalized by N-1 by default.
Use the mean to describe the sample with a single value that represents the center of the data. It depends upon the unit of measurement. Determine the mean the average of all the numbers by adding up all the data pieces xi and dividing by the number of pieces of data n.
Deviation this refers to the distance from the mean. Self careself efficacy had a difference of 178 1402-1224178 7. For the following sets of data calculate the mean and standard deviation of the data.
The higher deviation the more differences there are in the data set. Square each of those differences. Both and SD are descriptive.
The variance typically denoted as σ 2 is simply the standard deviation squared. In the second case we include exogenous monetary shocks but reduce their standard deviation to half of the historical estimate. We can obtain this by determining the standard deviation of the sampled mean which is the standard deviation divided by the square root of the total amount of numbers in a data set.
The simpliest interpretation could be. A low SD indicates that the data points tend to be close to the. If youre wondering What is the formula for standard deviation it looks like this.
It is rarely non-zero.
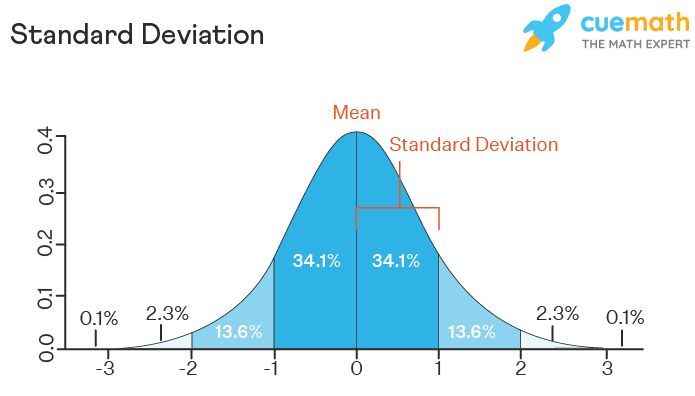
Standard Deviation Formula Definition Methods Examples

Ex Interpret The Mean And Standard Deviation Of Two Data Sets Youtube
0 Comments